怎么快速找到：附近的人

原文出处：怎么快速找到：附近的人

每周日下午，微信 simplemain ，老王又如约跟大家聊技术干货了。

想必大家都用过微信的“附近的人”这个功能，可以看到你周围都有谁，然后加个好友啥的。而我们出去吃饭，经常拿出大众点评，看看附近有哪些好吃的。更有，我们现在经常用 uber 或者滴滴打车，你发出一个路线请求，就有附近的司机来抢单。或者，当你用百词斩背单词的时候，可以找个附近的人 PK 单词量（哈哈哈，看到内置广告了吧 ~ ）

我们今天不讨论这个功能在产品上的意义，而是讨论讨论在技术上，他是怎么样来实现的。

好了，正式开始今天的话题吧 ~

关于经纬度

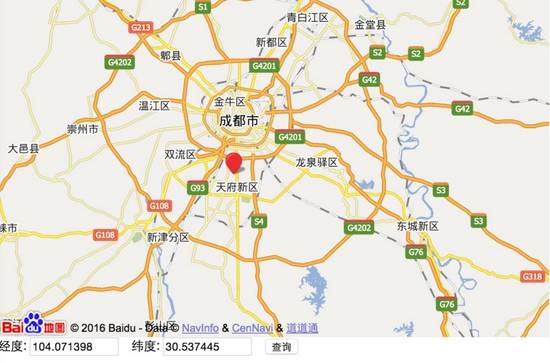
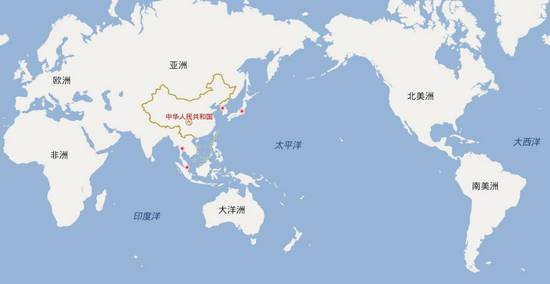
说到附近的人，第一个要谈到的就是经纬度。想必大家在初中（或者是高中）的地理课本里早就学过了。我们把地球分成横竖交错的一些格子，每个点都可以用横竖坐标来表示。横线表示纬度（范围在 [-90 ° , +90 ° ] ），竖线表示经度（范围在 [-180 ° , +180 ° ] ）。比如老王所在的位置，就可以在地图上用经纬度来表示：

如何获取经纬度

既然每个人所在位置都可以用经纬度来表示，那我们如何获取呢？我们现在智能手机基本都可以通过 GPS 或者基站进行定位，只要 app 调用系统的定位函数，就可以轻易拿到这样的数据（当然，需要用户的确认）。当客户端拿到这样的数据以后，就可以将位置信息上传服务器，由服务器来判定附近有哪些人。

如何查找

好了，该切入关键点了。当服务器收到很多用户的位置信息以后，怎么来判断你周围有哪些人呢？我们先想一个最简单的实现。当平面上只有两个点（分别代表两个人）的时候，我们怎么计算出他们之间的距离呢？

如果把地球看成一个球体，我们比较容易就用立体几何的知识去计算出他们之间的距离。但是这个过程会比较复杂。如果我们相距的两点不是特别远（相对地球半径而言），我们就可以把他们近似看成平面上的两点，用最简单的欧式距离公式 d(A,B) = sqrt((x1-x2)^2 + (y1-y2)^2) ，便可以得到 A 和 B 之间的距离，对吧。

好了，当我们的用户不是太多的时候，我们就可以采用遍历的方法，依次计算出其他所有的点同我的距离 d1 d2 ... dk ，然后按照距离从小到大排序，得到我们想要的结果，对吧？

看起来一切都很美妙，我们来算算时间复杂度。遍历所有的点，计算距离，是一个 O(n) 复杂度的算法，然后排序做 Top ，基本上是一个 O(n lgn) 的复杂度。所以，总的看来，是一个 O(n lgn) 复杂度的算法。当然，在计算和排序的过程中我们可以做优化。当在几千个点的时候，我们的服务器都可以轻松应对，如果我们的点变多了呢？比如，几万、几十万……

第一种方案：分布式计算

还记得以前老王讲分布式的文章（忘了的同学请到老王的微信 simplemain 里寻找哈）嘛？

很显然涉及到大量运算的时候，我们可以将这些运算拆分到多个服务器来进行，这样就可以提高我们并行计算的速度和效率。那当我们有几万、十几万用户的时候，我们就可以将这些用户分布到不同的机器上，让每个机器都计算一部分，然后每个机器给出自己机器的 Top ，最后由某一台或几台汇总，给出最后的结果。

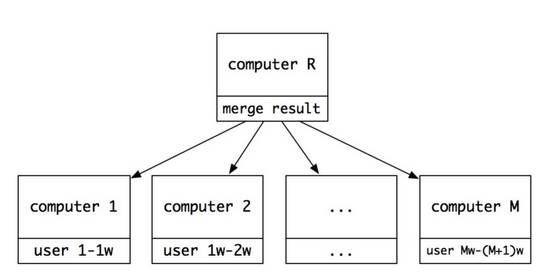
比如，第一台机器计算 uid 从 1-10000 的用户和我的距离，并给出最后的 top100 ；第二台机器计算 uid 从 10001-20000 的用户和我的距离，并给出最后的 top100 ……以此类推。最后由 computer-R 来汇总这些 top100 ，并给出排序结果，输出最后的 top100 。

如果当计算的机器特别多， computer-R 就会成为瓶颈，就需要分裂成多台机器，然后再汇总。

这种方案的优点就是：

1 、算法实现简单：只需要用单机版的点点距离判断 + 排序，就可以搞定；

2 、前面的结果相对比较精确：因为距离都是非常精确的欧式距离，所以 TopK 的结果都是比较精确的

不足：

1 、消耗机器严重：随着用户量的增加，机器消耗就直线上升；

2 、后面的结果相对不那么精确：在每台机器做 TopN 以后，实际上就扔掉了其余的数据，最后有可能某台机器上一个很优的结果，没有进入到最后的归并排序。

#第二种方案： GeoHash

那我们有没有办法降低对机器的消耗，而且还能在全局做到相对准确的结果排序呢？

其实也是有办法的。具体怎么做呢？跟着老王一起往下看吧。

what to do ？

如果我们能将地球划分成一个个很小的方形的格子，在同一个格子里的人，是不是就很接近呢？再如果，我们给每个格子编一个代号，那拥有同一个代号的人，是不是就靠的很近呢？这有可能么？那我们就来试试吧 ~

how to do ？

1 、把地球拉成平面：

先假设我们把地球从一个球体拉成一个平面（用几何知识就可以求解相关的对应关系）。

2 、按经度将地球切开

我们以经度 0 °为中轴，将地球切成两半 [-180 ° ,0 ° ),[0 °， 180 ° ] ，并对他们进行二进制编码，左边为 0 ，右边为 1 。

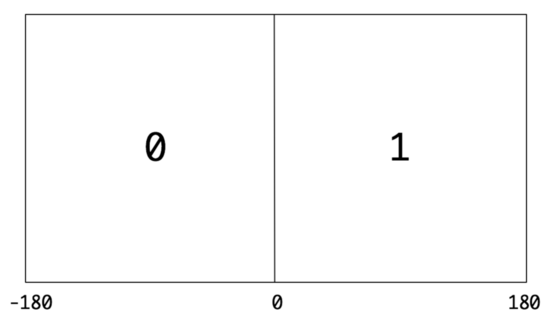
那所有经度坐标在左边的，都得到了 0 这个编码，而其他的则得到 1 这个编码。比如，老王所在位置的经纬度值是 (104.071398, 30.537445) ，老王的经度 104.071398 ∈ [0 °， 180 ° ] ，所以编码就是 1 。

好了，接下来我们就进行第二次切割，还是按照老规矩，我们把现有的两个部分也分别切割成左右两个部分，于是得到这样的一个图：

我们得到四个编码： 00 01 10 11 ，每个编码的第一位是第一次切割时候得到的数字， 0 0 0 1 就是第一切割时在左边，编码为 0 ；第二位就是第二次切割，在左边为 00 ，在右边为 01 。同理得到 10 11 。比如，老王所在位置的经纬度值是 (104.071398,30.537445) ，老王的经度 104.071398 ∈ [90 °, 180 ° ] ，所以编码就是 11 。

如此这样重复 N 次，我们就可以将地球按经度切割成很多很多的小块，如果切割的次数足够多，那同一个经度值的人，都会在同一个小块儿里，对吧。那也会得到对应这个小块儿的二进制编码。比如老王的经度 104.071398 经过多次切割得到如下这个表格：

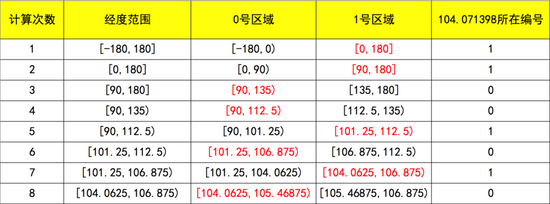
这样，我们就可以得到 104.071398 的编码是： 11001010 。随着切分的继续，我们可以得到更长的编码，这样就可以对应更细致的区间。

3 、按纬度将地球切开

用同样的方法，我们按照纬度也把地球切成这样的方式，最终得到对应经纬度的编码：

(104.071398, 30.537445) -> (11001010,10101011)

老王简单写了一个编码的实现代码：

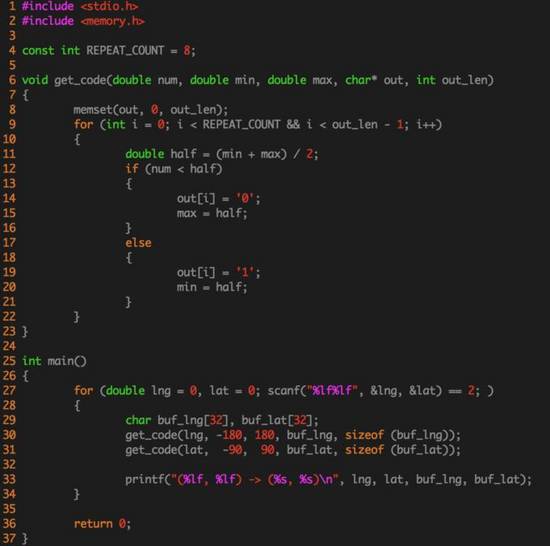
有了经纬度的切割，地球就被我们划分成了 2 n *2 n 个格子，比如当 n 等于 8 的时候，这个格子数就是 65536 。

4 、统一编码

为了方便记录，我们把经度和维度的二进制格子编码进行合并，按经度、纬度、经度、维度……这样的顺序，一位一位的进行放置：

(104.071398, 30.537445)

-> ( 11001010 ,10101011)

-> 1 1 1 0 0 1 0 0 1 1 0 0 1 1 0 1

上面最后的编码，奇数位的红色是经度编码，偶数位的黑色是纬度编码。这样表示起来还是太长了，我们怎么样缩短呢？也很简单，我们可以用 16 进制、 32 进制、 64 进制这样的进制来缩短编码长度。这里业界推荐的是 32 进制，也就是 base32 编码。

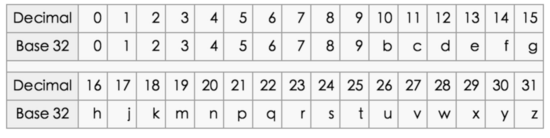
这样，每 5 个二进制（ 2 5 =32 ）组成一个编码字符，于是：

(104.071398, 30.537445)

-> (11001010, 10101011)

-> 1 1 1 0 0 1 0 0 1 1 0 0 1 1 0 1

-> wm6 (3 个完整有效进制数 )

5 、划分的精细度

有了这样的编码，那到底要划分多少次，我们的数据才足够精确呢？我们在维基百科上找到了这样的一张对应表：

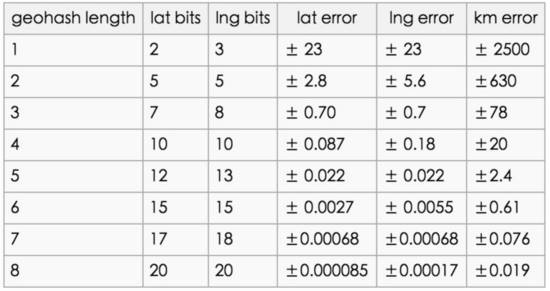
当有一个 base32 数字的时候，精细度大概是 2500 公里，当有 8 个数字的时候，精细度大概是 0.019km = 19 米。也就是说， 8 个 base32 的数字对应 8*5=40 个二进制数，也就是经纬度分别划 20 次，就可以达到 19 米的精细度。这对于我们平时使用已经足够了。

6 、如何查找

有了以上的准备工作，我们就可以给地图上所有的人进行编码了，然后将 (user,code) 这样的 key-value 对放入到数据库的 userloc_code 表中。当请求某个人附近的人的时候，我只要把这个人的 code 取出来，然后做一个 sql ： select * from user_loc_code where code=xxx 就可以得到想要的答案了（不过记得要在 code 上建索引哦 ^^ ）。这个算法的时间复杂度就完全取决于数据库的索引结构（如果是 Hash 索引，则近似 O(1) 算法；如果是 B-Tree 索引，则近似 O(lgn) 算法）。是不是很简单也很高效呢？

稍等！事情还没完呢。如果这个小方形里没有其他人怎么办？产品经理说：我们还是需要给用户返回最近的人！

那其实也很简单，我们只要把编码长度从 1 到 8 的编码都记录下来，我们就拥有了 2500km-0.019km 范围差的所有值，那我们写 sql 的时候，最多写 8 个，就一定能找到我们想要的（一般产品经理会说：我们只要 20 公里范围内的用户，那 sql 最多最多就只需要写 5 个，对吧）。具体的表就可以这样建：

(user, code1, code2, ..., code8) ，记得给每个 code 加上索引哦 ~

7 、话外音

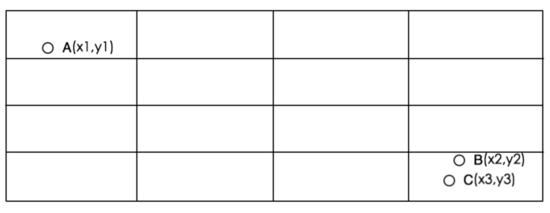
上述的算法，实际上是一个近似算法，我们认为在同一方形格子里的，就是距离最近的，可是实际上呢？

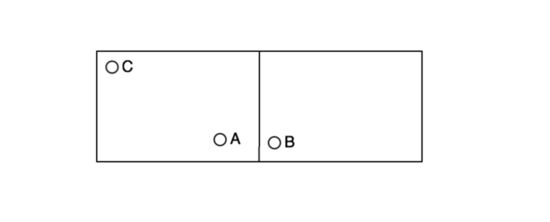
比如， A 和 C 在同一格子里， A 和 B 在不同格子里，但是明显 A 和 B 的距离更近，但是却被硬生生的分开了…… 那这种问题我们如何来解决呢？其实也是有办法的。

如果产品要求不高，我们就不需要解决。如果产品确实要求精度比较高，我们可以取求解的格子的周围其他八个格子的点，然后一起来算距离排序。这样，我们就能求解到最精确的值。

原文出处：怎么快速找到附近的人续

一.背景说明

首先，非常感谢 简单的老王 给我们做了一个相当有料的技术方案分享《怎么快速找到：附近的人》，如果您想往下了解，请先阅读老王的文章。

其次，本文的内容仅仅是在老王的启示下想到的方案，并未在某个具体的项目中使用过，在这里也是跟大家探讨可行性。

正如老王结尾所说，_GeoHash_方式也会有弊端，比如，A和C在同一格子里，A和B在不同格子里，但是明显A和B的距离更近，但是却被硬生生的分开了……

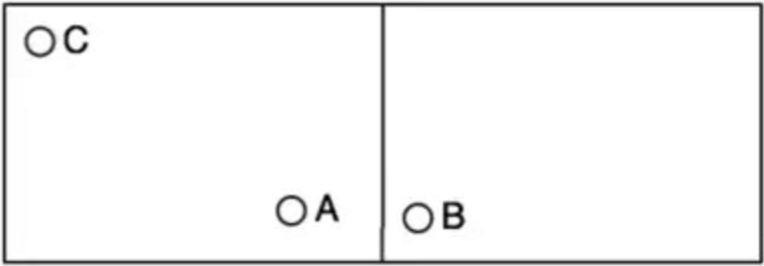
那有没有一种其它方式来寻找附近的人呢？

二.内切圆寻找法

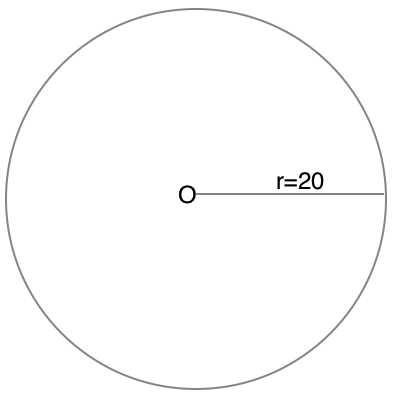
1.以当前用户的坐标为圆心画圆

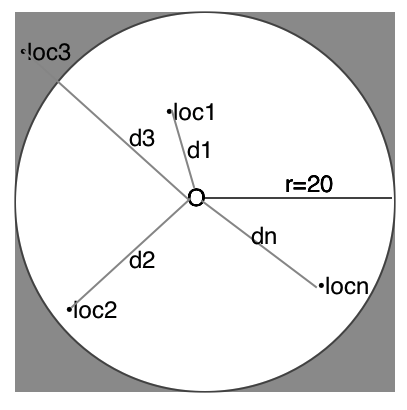
例如：以O(104.07139898,30.53744565)作为圆心，半径r=20(m)画圆。这里的半径就根据项目的实际需求确定，假如PM要求附近500m以内的人，那么r=500。

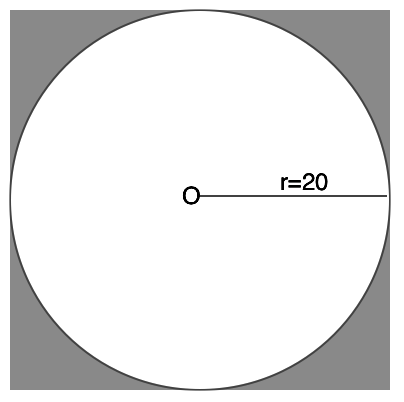
2.以圆的外切正方形为基础区域

这时候坐标位于圆形区域里的用户，就是附近的人，但是由于圆所占有的区域比较起来不是很舒服，我们考虑把圆的外切正方形作为目标区域。处于该正方形内的用户，就是我们所要寻找的用户User(1...n)。

3.距离转化为经纬度范围

我们所设半径r=20(m)，这时候需要把20m转化为坐标系单位。

赤道一周为40076000m，纬度是（W180，E180）,由此估算纬度上1m≈0.00000898度（360/40076000）；
子午线长度为 40009000m，经度是(N90,S90), 由此估算经度上1m≈0.00000450度（180/40009000）。

所以外切正方形所覆盖的区域经纬度范围为
(104.07139898±(0.00000898 ⅹ 20), 30.53744565±(0.00000450 ⅹ 20))。

4.查找该范围内的用户

此时，我们已经拿到了目标用户的经纬度，就去数据库中查找
SELECT * FROM USER_COORDINATE WHERE (long>=long1 and long<=long2) or (lat>=lat1 and lat<=lat2) 此时得到一组目标用户的位置Locations(loc1(long1,lat1)...locn(longn,latn))

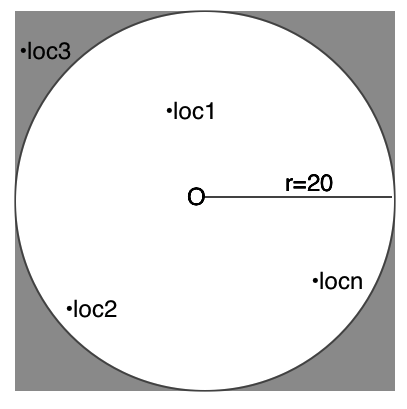
5.计算所查用户与当前用户的距离

把Lcocations与圆点坐标O代入欧式距离公式d(A,B) = sqrt((x1-x2)^2 + (y1-y2)^2) 得到一组距离d(d1,d2....dn)。
再对d进行排序，即可由近及远的得到附近的人。

三.内切圆寻找法的进一步分析

1.对经纬度的精度要求比较高

在上面的过程中也看到了，在单位米转化为度的过程中，得到的经纬度是1e-6级别(微米级别)，因此我们在获取利用GPS获取用户的坐标时，需要一个较高的精度。

2.单位米转化为经纬度标准是不同的

我们知道，赤道，回归线，级圈线的周长是不一样的，也就是有个反比关系：纬度越高，所处的周长越短。所以我们在把单位米转化为度的时候，要实际参考当前纬度坐标，才能得到具有意义的值。

纬线长基本满足这么个公式：

纬线长＝ 2 * π * COS（纬度）*（地球半径）

由此我们可以大概算出当前用户所处纬度的纬线长L，然后算出米与度的转化：

1m≈ (360/L)

同理可计算出经度上的米与度的转化关系。

3.数据库查找目标用户

众所周知，数据库的操作是毫秒级别的，所以我们根据经纬度范围去数据库找目标用户，是一个很快的过程，不存在效率问题。如果用户群达到千万级别，可以通过优化存储表来提高效率。

4.时间复杂度

我们通过目标用户的坐标Lcocations去计算与当前用户的距离时，时间复杂度为O(n)。排序的时间复杂度可以参考下图。