原文出处：声音的表示（1）

（本文基本逻辑：声音的定义是什么 → 声音有哪些特征 → 怎样对声音进行数学描述 → 怎样对声音进行数字化 → 数字音频数据是什么）

『声音』是我们司空见惯再熟悉不过的一种物理现象。我们唱歌发出声音，用耳朵听到声音，用手机记录并分享声音；如果作为音视频开发人员，我们还会在工作中处理众多声音数据。但是，你真的了解『声音』吗？

如果你自信满满，心想『当然了』，那可以试试回答这个问题：从我们耳朵听见的『声音』，到我们用手机、电脑所处理的『音频数据』，其中经历了什么？如果你细思起来，感觉还有疑问，不妨继续读下去，和我们一起略略探讨一下：日常开发工作中处理的音频数据，是如何从一种物理现象转变而来。这个探讨也许无用，但可能会有趣。

探讨这个问题，至少包含了两个大的认知过程：1）用科学研究的方法对一个日常现象进行物理定义、特征探索、规律发现、数学描述的过程；2）用信息处理手段对物理现象进行数字化的过程。

当我们用这样的视角回头去看这个问题时，也许可以把它细分成下面几个子问题：

1、声音的定义是什么？

『声音』是振动产生的声波，通过介质（气体、固体、液体）传播并能被人或动物听觉器官所感知的波动现象。

以上便是声音的定义，它将声音界定为一种波动现象，这样就可以针对性的在『波』这个物理概念的范畴里去研究它。当然，如果我们在研究中有新的发现，能颠覆原有的认知，从而重新定义它，也不是没有可能。

2、声音有哪些特征？

要提取声音的特征，首先要感知到它，人类的听觉感知系统是一个复杂的系统，如下图所示。它是怎么感知声音的呢？简单来讲，声音作为一种机械波，通过空气传播到人耳，在人耳中转变为神经动作电位，神经脉冲到达大脑，人从而感知到声音。至于具体细节，我们就不在这里做过多探讨了。

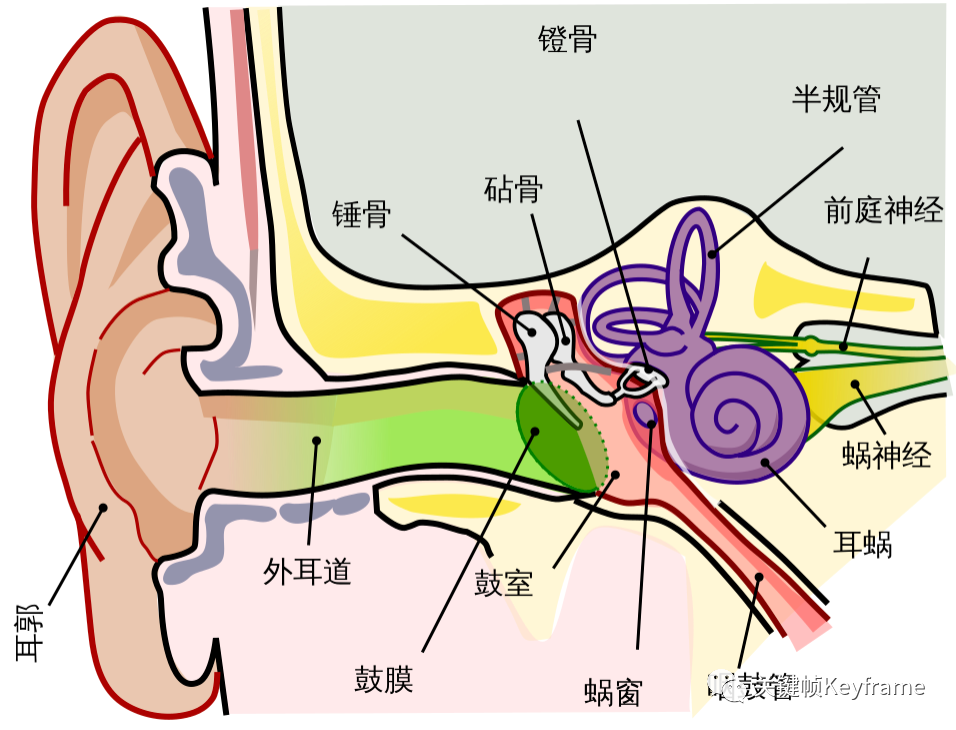
声音的特征是我们在感知声音并不断对其现象进行研究的过程中逐步识别和提取出来的。比如，我们很容易就能感知到声音有大有小；有尖锐有浑厚；不同的人说话，即使声音大小差不多，我们也能识别他们。我们对这些感知进行总结便提取出了声音的特征。

现在我们都知道，声音的特征就是大家熟知的『声音三要素』：

基于声音的特征继续研究下去，我们还可以发现与之相关的规律和因果关系，并通过一些手段来形象化的展示它们。

比如，我们通常听见的声音，是由于物体振动导致空气分子按照一定的频率产生疏密相间的排列而传播。

当我们取一个单点，来测量这个点的气压随时间的变化，用横轴表示时间，纵轴表示气压，我们可以得到类似下面这张波形图：

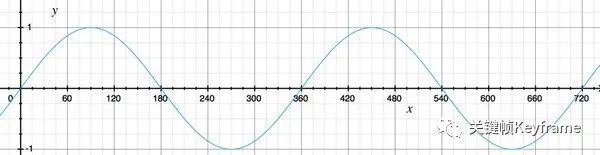
气压距离标准值偏差越大，说明振动越剧烈，所以振幅越大的波形表示声音越大，即响度越大。波形越紧密说明单位时间内振动的次数越多，频率越高，即音调越高。

对于上图这样单频率的振动，通过波形图来看声音的相关信息是很简单明了的。而实际情况中，我们听到的声音往往是复杂振动的叠加，比如下图这样：

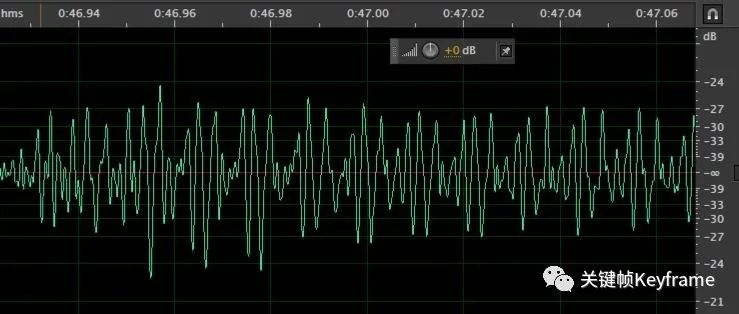
通过这个波形图，我们很难看出声音的有效信息，因为各个频率的波形都叠加在一起了。这时候我们就需要借助频谱图来帮忙了。

频谱图是怎么来的呢？我们可以看看下图：

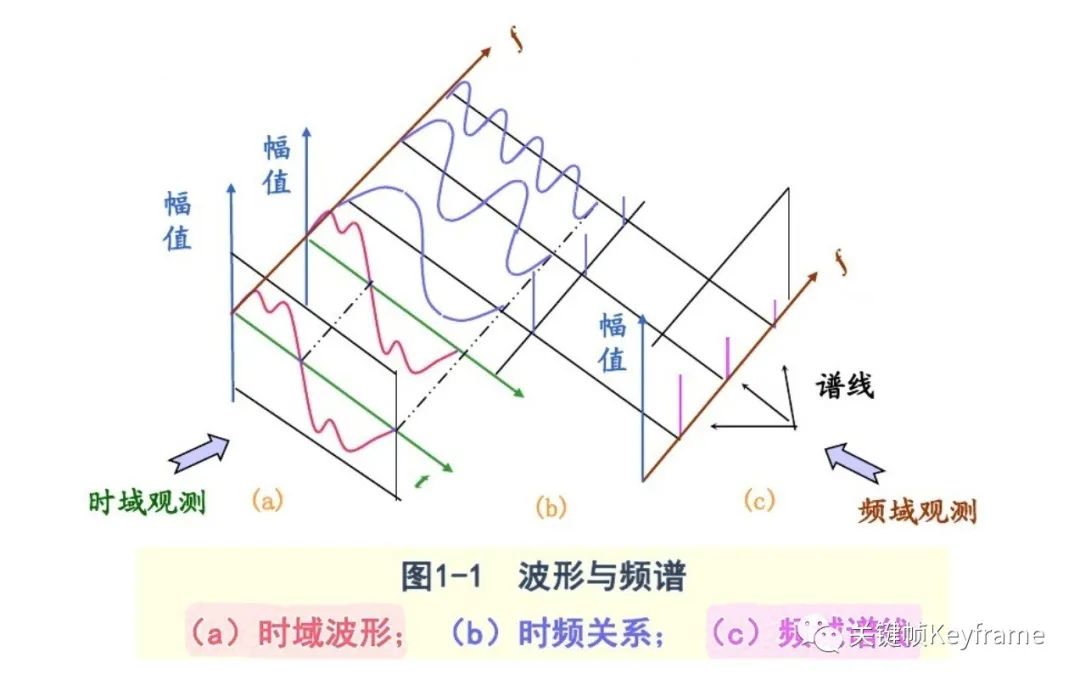
波形可以由多个频率、不同振幅和相位的简单正弦波复合叠加得到的。波形图的横坐标是时间，纵坐标是振幅，表示的是所有频率叠加的正弦波振幅的总大小随时间的变化规律。

将该复合波形进行傅里叶变换，拆解还原成每个频率上单一的正弦波构成，相当于把二维的波形图往纸面方向拉伸，变成了三维的立体模型，而拉伸方向上的那根轴叫频率，现在从小到大每个频率点上都对应着一条不同幅值和相位的正弦波。

频谱图则是在这个立体模型的时间轴上进行切片，形成的以横坐标为频率，纵坐标为幅值的图形。它表示的是一个静态的时间点上，各频率正弦波的幅值大小的分布状况。

波形图可以帮助我们检查音乐整体音量的大小，在混音中常常可以看出动态和响度等问题，可以用来辅助调节压缩器和限制器。频谱图则可以帮助我们定位音乐细节在各频段上的分布问题，在混音中可以用来辅助调节滤波器和均衡器。

下图是一个声音的波形图（上部分）和频谱图（下部分）的示例：

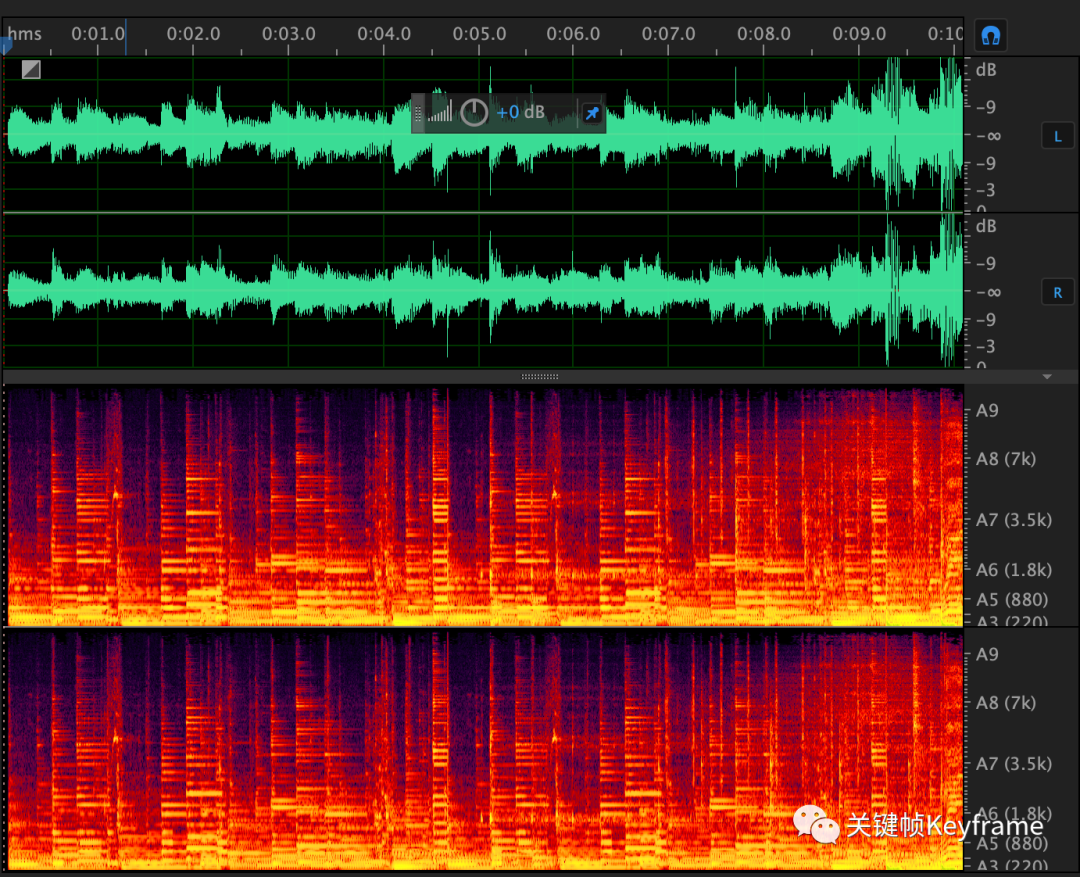
其中，波形图比较简单，横轴是时间，纵轴是响度，并区分了左右声道。

但频谱图相对我们上面讲的定义要更复杂一些了，这里的频谱图是一个三维图，其中横轴是时间，纵轴是频率（这里用了音调表示，比如 A5(880) 对应的频率是 880Hz），颜色亮度表示响度。所以频谱图相对于波形图，是包含有更多信息的，唯一的缺点就是无法表示整体音量的大小，所以一般和波形配合使用来辨别声音特征。

（通过上文的探讨，我们知道了声音是一种波动现象，了解了声音有响度、音调、音色几个特征，还初步接触了研究声音时的辅助工具：波形图和频谱图。对于声音的数学描述的 问题，我们将在后面继续探讨，敬请期待）

原文出处：声音的表示（2）

『声音』是我们司空见惯再熟悉不过的一种物理现象。我们唱歌发出声音，用耳朵听到声音，用手机记录并分享声音；如果作为音视频开发人员，我们还会在工作中处理众多声音 数据。但是，你真的了解『声音』吗？

在前面的文章《声音的表示（1）》里，我们提出了一个问题：从我们耳朵听见的『声音』，到我们用手机、电脑所处理的『音频数据』，其中经历了什么？从这个问题出发，我们探讨了『声音的定义是什么』和『声音有哪些特征』这两个问题，接下来我们继续探讨下个问题：『怎样对声音进行数学描述』。

3、怎样对声音进行数学描述？

有了声音的定义，也明确了声音的特征，那接着便可以探讨对特征的数学描述了。

3.1、响度的数学描述

响度是反映人耳感受到的声音强弱的主观心理量，根据它可以把声音排成由轻到响的序列。

对应的，与声音强弱相关的客观物理量有『声强』、『声压』等。而要理解声强，先要理解一下『声能』的概念。

声能是声音在介质中传播时，使媒介附加的能量。由于声波是质点偏离平衡位置的振动，所以声能定义为质点振动动能和质点偏离平衡位置所具有的势能的总和，单位是『瓦(W)』。

声强是单位时间内通过垂直于声波传播方向的单位面积的平均声能，用 I 表示声强。声强的单位是『瓦/平方米(W/m²)』。人耳允许的声强范围为 0.000000000001~1 W/m²，这个范围太大。此外，心理物理学的研究表明，人对声音强弱的感觉并不是与声强成正比，而是与其对数成正比的，所以我们引入『声强级』来表示声强。

虽然声强在理论上可以客观衡量在某一点上的声波振幅，还可以通过测量得出其数值，但并不是一个在日常工作中经常用来阐述声音振幅的量。由于人耳表现为压力敏感组织，又因为压力或压强具有相对容易进行实地测量的特点，所以目前实际中更多是使用声压来代表声波的振幅表现。

声压是指声波通过媒质时，由振动所产生的压强改变量，单位是『牛顿每平方米(N/m²)』或『帕斯卡(Pa)』，用 P 表示声压。声音在空气中传播时，物体的振动带动周围空气的振动，形成了疏密相间的波动，所以压力变化增量是正负交替的。通常取声压的均方根值，称为有效声压。如未说明，通常所指的声压即为有效声压。声压范围为 0.00002~20 N/m²，这个范围太大，同样的，人对声音的强弱的感觉是与声压的对数成正比，所以我们引入『声压级』表示声压。

声压与声强的关系：在自由声场中，某处的声强与该处声压的平方成正比，与介质密度与声速的乘积成反比。

所谓级是做相对比较的无量纲量。例如声强级和声压级等。

声强级（Sound Intensity Level，SIL），是以 10-12 W/m² 为参考值，任一声强与其比值的对数乘以 10 记为声强级，单位是『分贝(dB)』。这里为什么乘以 10？这个是由『贝尔』和『分贝』两个单位的定义而来，贝尔这个单位太大，这样计算得到的数值就相对较小；所以取其十分之一为单位『分贝』，来放大计算的数值，更容易体现数值之间的差异。

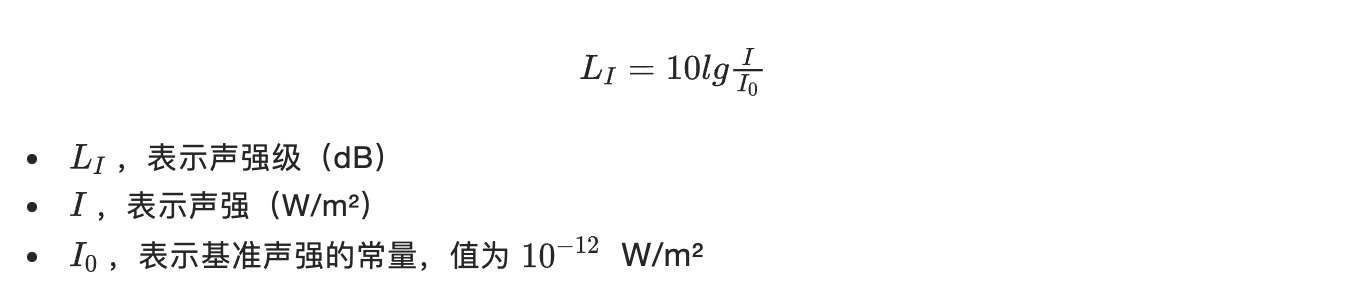
声压级（Sound Pressure Level，SPL），是以 2×10-5 N/m² 为参考值，任一声压与其比值的对数乘以 20 记为声压级，单位也是『分贝(dB)』。这里为什么是 20？把上面讲到的声压与声强的关系公式带入进声强级的计算公式即可推到得出声压级的计算公式。

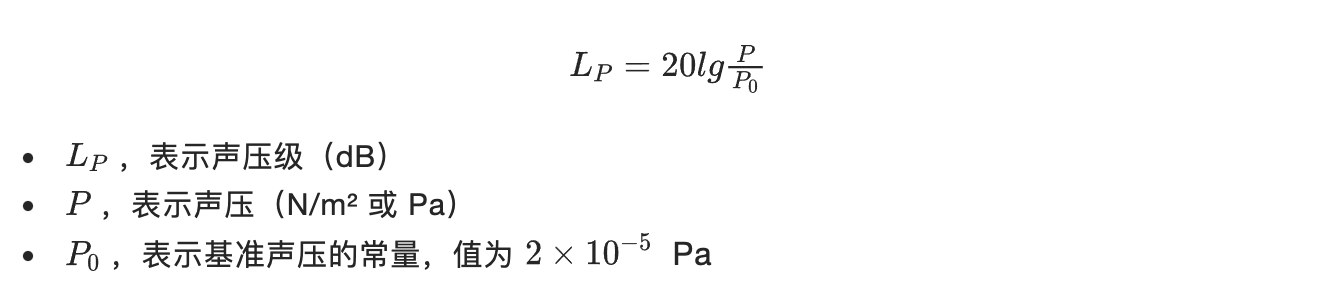
人耳对声音的感觉，与声压有关，但也不是只与声压有关，还和频率有关。声压级相同，频率不同的声音，听起来响度也不同。

为了在数量上估计一个纯音的响度，可以把这个纯音和 1000 Hz 的某个声压级的纯音在响度上作比较。这两个声音在听觉上认为是相同的响度时，就可以把 1000 Hz 纯音的这个声压级规定为该频率纯音的响度级。响度级的单位为『方(Phon)』。

举例来说，一个纯音的频率 1000 Hz，若希望其响度能达到 40 方，根据等响度曲线图，其声压级就必须达到 40 dB SPL。

下图中，横坐标为频率，纵坐标为声压级，波动的一条条曲线就是等响度曲线（equal-loudness contours），这些曲线代表着声音的频率和声压级在相同响度级中的关联。

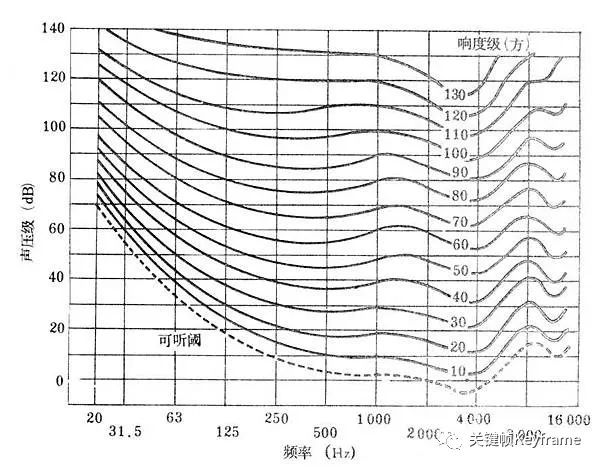
响度级既考虑了声音的物理效应，又考虑了人耳的听觉生理效应，表示人耳对声音的主观评价。

我们日常所说的分贝指的是声压级。比如：

1 分贝
刚能听到的声音
15 分贝以下
感觉安静
30 分贝
耳语的音量大小
40 分贝冰箱的嗡嗡声
60 分贝正常交谈的声音
70 分贝相当于走在闹市区
85 分贝汽车穿梭的马路上
95 分贝摩托车启动的声音
100 分贝装修电钻的声音
110 分贝卡拉 OK 的声音
120 分贝‍飞机起飞时的声音
150 分贝燃放烟花爆竹的声音

比如上表所说的，飞机起飞时的声音是 120 分贝，如果我们知道对应的声音的频率，我们就能知道它的响度级。

3.2、音调的数学描述

音调是人耳对声音高低的主观感受。音调对应的客观评价尺度是声波的『频率』。音调的高低是由振动频率决定的，两者成正相关关系。

频率的计量我们比较熟悉，单位是『赫兹(Hz)』。那么音调是怎么计量呢？一种计量法是将音调的单位称为『美(mel)』，取频率 1000 Hz、声压级为 40 dB 的纯音的音调作标准，称为 1000 mel，另一些纯音，听起来调子高一倍的称为 2000 mel，调子低一倍的称为 500 mel，依此类推，可建立起整个可听频率内的音调标度。

乐音（复音）的音调更复杂些，一般可认为主要由基音的频率来决定。

音调和频率的对应关系如图：

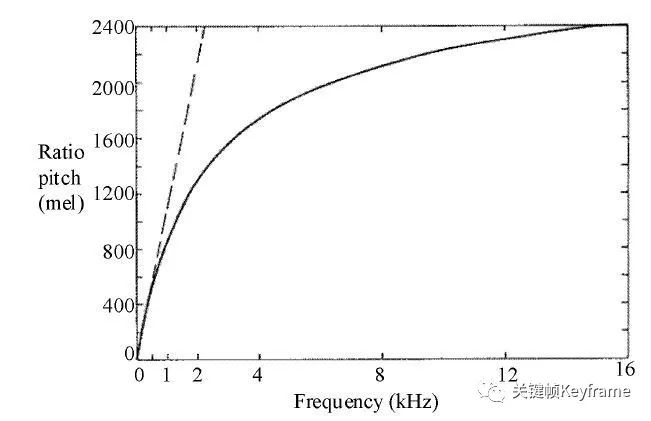
在 500 Hz 以下，音调和频率基本上近乎成线性关系，但是对于中高频则成对数关系。

此外，音调通常使用『科学音调记号法』或使用结合字母与数字（用以表示基频）而成的记录法。

两个音符之间若频率相差整数倍，则听起来非常相似。因此，我们将这些音放在同一个『音调集合』中。两个音符间若相差一倍的频率，则我们称两者之间相差一个八度。要完整描述一个音符，则必须同时说出它的类别以及它在哪个八度之中。在传统音乐理论中，我们使用前七个拉丁字母：A、B、C、D、E、F、G（按此顺序则音调循序而上）以及一些变化（详情请见下文）来标示不同的音符。这些字母名字不断的重复，在 G 上面又是 A（比起前一个 A 高八度）。为了标示同名（在同一个音调集合中）但不同高度的音符，科学音调记号法（scientific pitch notation）利用字母及一个用来表示所在八度的阿拉伯数字，明确指出音符的位置。比如说，现在的标准调音音调 440 赫兹名为 A4，往上高八度则为 A5，继续向上可无限延伸；至于 A4 往下，则为 A3、A2 等。传统上，由于历史原因，八度的数字标注由 C 音符开始，结束于 B：C、D、E、F、G、A、B（按此顺序则音调循序而上）。

有时我们也会在音名旁加上变音记号，如升号和降号。这些符号代表将原音升高或降低半音，在十二平均律（现在最广泛使用的调音法）中则是将原频率乘或除以 2(1/12)=1.0594 倍，即升高 n 个半音就将原频率乘 2(n/12) 倍，降低 n 个半音则乘 2(-n/12) 倍。升音符号为 ♯，降音符号则为 ♭。它们通常写在音名之后，如 F♯ 表示升 F，而 B♭ 表示降 B。其它的变音符号如重升或重降（将原音升高或降低一个全音，即两个半音），在传统乐理中也会用到。在等音音程（enharmonicity）的情况下，我们可以利用变音记号把同一个音调记成不同的音符。举例而言，把 B 升半音成为 B♯，其实就与 C 同音。不过，在删去这些异名同音的情况后，完整的半音音阶在原来的七个音上添加了五个音调集合，且任两个相邻的音调集合都相差半音。

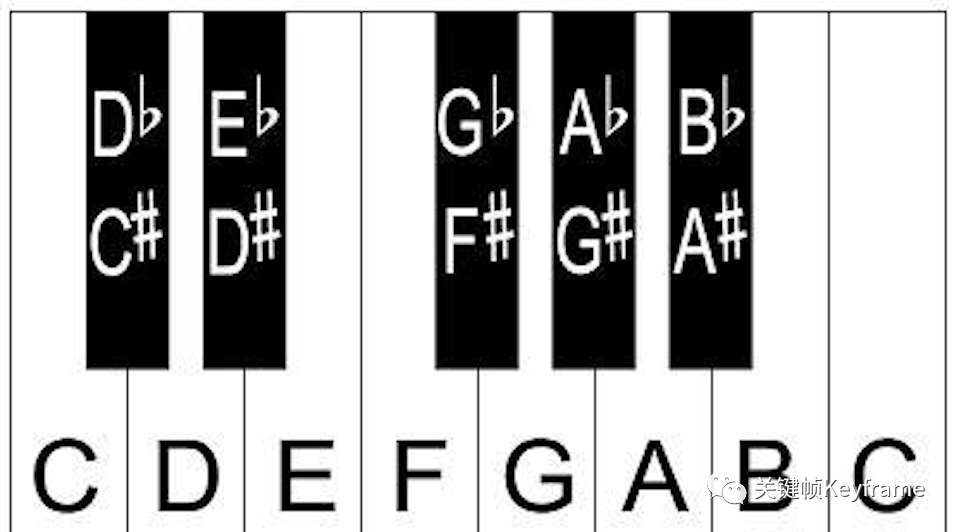
注意，7 个全音只有 5 个半音。E 和 F 之间，B 和 C 之间是没有半音的。详细来讲，就是一个八度之间有 12 个半音。其中 7 个（CDEFGAB）叫自然音，另外 5 个叫变化音。自然音之间一般是隔着两个半音（相隔两个半音可以叫距离为一个全音），也有部分自然音之间（E 和 F，B 和 C）只隔一个半音。

下面的图表完整的表示自 C4（中央 C）起向上八度内的半音音阶：

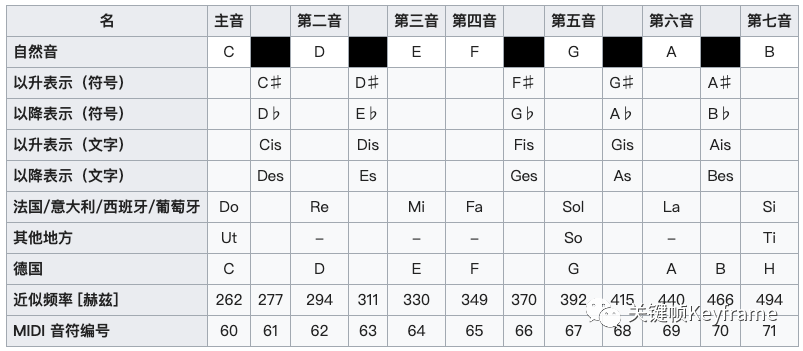
常见的国际谱、男唱谱、女唱谱的部分记号和频率对照表：

国际谱男唱谱女唱谱频率
C0C1C216.35
C♯0/D♭0♯C1♯C217.32
D0D1D218.35
D♯0/E♭0♯D1♯D219.45
E0E1E220.6
F0F1F221.83
F♯0/G♭0♯F1♯F223.12
G0G1G224.5
G♯0/A♭0♯G1♯G225.96
A0A1A227.5
A♯0/B♭0♯A1♯A229.14
B0B1B230.87
C1CC132.7
C♯1/D♭1♯C♯C134.65
D1DD136.71
D♯1/E♭1♯D♯D138.89
E1EE141.2
F1FF143.65
F♯1/G♭1♯F♯F146.25
G1GG149
G♯1/A♭1♯G♯G151.91
A1AA155
A♯1/B♭1♯A♯A158.27
B1BB161.74

3.3、音色的数学描述

声音的响度表示声音的大小，音调表示声音的频率，这两个还是比较好理解的。

那么怎么理解声音的音色呢？

现实中声音的波形绝大多数都不是简单的正弦波，而是一种复杂的波。这种复杂的波形可以分解为一系列的正弦波，这些正弦波中有基频 f0，它对应声音的基音，还有与 f0 成整数倍关系的谐波：f1、f2、f3、f4 等，它们对应声音的泛音，它们的振幅有特定的比例。这种特定的比例，赋予每种声音特色，这就是音色。如果没有谐波成分，单纯的基频正弦信号是毫无音乐感的。因此，乐器乐音的频率范围包括基频和谐波。

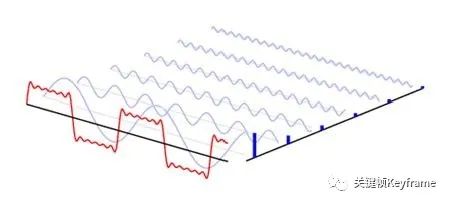
上一节讲到的声音音调的高低是由基音对应的基频决定的。这就是为什么同唱一个音调，不同人的音色截然不同的根本原因：他们只是基频相同，谐波是截然不同的。

所以，声音的音色决定于谐波频谱，也可以说是声音的波形所确定的。

（通过上文的探讨，我们知道了如何对声音的响度、音调、音色特征进行数学描述。在这个过程中，引入了众多的物理量和概念：比如与响度相关的声能、声强、声压、声强级、声压级、响度级等；与音调相关的频率、科学音调记号法、十二平均律等；与音色相关的基频、基音、谐波、泛音等。这些物理量和概念是对声音进行数学描述的工具和桥梁，而基于这些物理量和概念建立起来的数学模型是我们对声音数字化的基础。对于声音数字化的问题，我们将在后面继续探讨，敬请期待）

原文出处：声音的表示（3）

『声音』是我们司空见惯再熟悉不过的一种物理现象。我们唱歌发出声音，用耳朵听到声音，用手机记录并分享声音；如果作为音视频开发人员，我们还会在工作中处理众多声音数据。但是，你真的了解『声音』吗？

在前面的文章里，我们提出了一个问题：从我们耳朵听见的『声音』，到我们用手机、电脑所处理的『音频数据』，其中经历了什么？从这个问题出发，我们在《声音的表示（1）》和《声音的表示（2）》两篇文章中探讨了『声音的定义是什么』、『声音有哪些特征』、『怎样对声音进行数学描述』这几个问题？接下来我们继续探讨另外两个问题：『怎样对声音进行数字化』和『数字音频数据是什么』。**

4、怎样对声音进行数字化？

对声音进行数字化，首先要使用特定的设备对声音进行采集，比如麦克风就是常见的声音采集设备。麦克风里面有一层碳膜，非常薄而且十分敏感。声音是一种纵波，会压缩空气也会压缩这层碳膜，碳膜在受到挤压时也会发出振动，在碳膜的下方就是一个电极，碳膜在振动的时候会接触电极，接触时间的长短和频率与声波的振动幅度和频率有关，这样就完成了声音信号到电信号的转换。之后再经过放大电路处理，就可以实施后面的采样、量化处理了。

上面探讨了声音三要素的数学描述，这是声音数字化的基础。

声音由波形组成，包含了不同频率、振幅的波的叠加。为了在数字媒体内表示这些波形，需要对波形进行采样，其采样率需要满足可以表示的声音的最高频率；同时还需要存储足够的位深，以表示声音样本中波形的适当振幅。

声音处理设备重建频率的能力称为其频率响应，创造适当响度和柔度的能力称为其动态范围，这些术语通常统称为声音设备的保真度。最简单的编码方式可以利用这两个基本元素重建声音，同时还能够高效地存储和传输数据。

声音的数字化过程是将模拟信号（连续时间信号）转化为数字信号（离散时间信号）的过程，包括 3 个步骤：

其过程如下图所示：

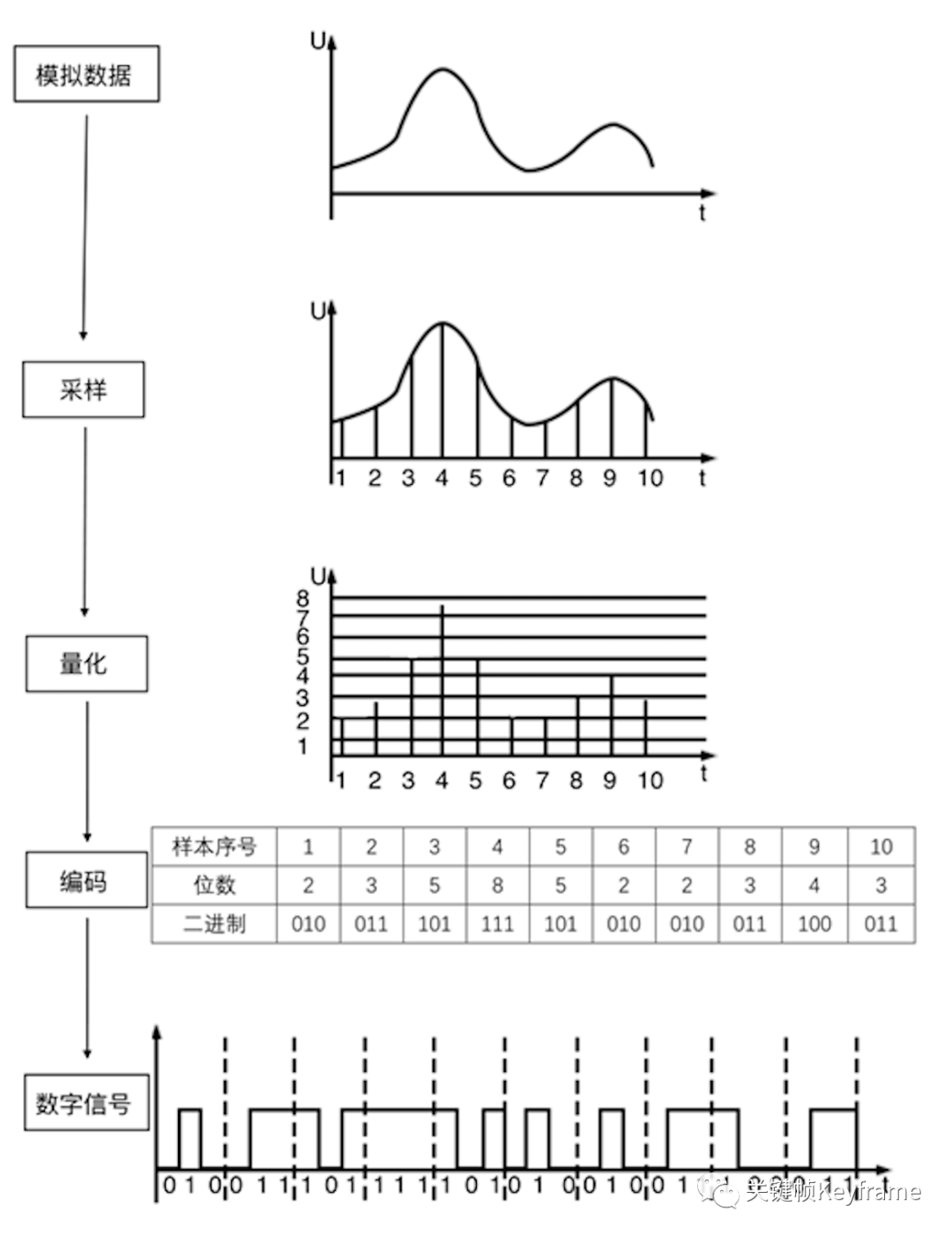
经过数字化处理后的数字音频包含如下三要素：

1）采样率

对模拟信号的采样一般遵循奈奎斯特采样定理：如果一个信号是带限的（即它的傅立叶变换在某一有限频带范围以外均为零），并且它的样本取得足够密（相对于信号中的最高频率而言），那么这些样本值就能唯一地用来表征这一信号，并且能从这些样本中把信号完全恢复出来。为了不失真地恢复模拟信号，采样频率应该不小于模拟信号频谱中最高频率的 2 倍。一般实际应用中保证采样频率为信号最高频率的 2.56～4 倍。

数字信号由模拟信号采样而来，如果满足采样定理，数字信号就可以完全恢复原始的模拟信号。

从发声的角度来看，人类发出的声音信号频率绝大部分在 5k Hz 以内，因此以 10k Hz 的频率来采样就足够了。

从听声的角度来看，人类听觉范围是 20～20k Hz 内的音频，那么数字音频的采样率需要在 40k Hz 以上。

CD 音频使用 44100 Hz 的采样率，部分原因也在于此，至于为什么具体是 44100 这个数字，这个是历史原因：最早的数字录音由一台录像机加上一部 PCM 编码器制作的，由于当时使用的是 PAL 录像制式（帕制，与之对应的有 NTSC），场频 50 Hz，可用扫描线数 294 条，一条视频扫描线的磁迹中记录 3 个音频数据块，把它们相乘，就得到了 44100 这个奇葩数字。

生活中常见的采样率：

8,000 Hz：电话所用采样率，对于人的说话已经足够；
11,025 Hz：AM 调幅广播所用采样率；
22,050 Hz 和 24,000 Hz：FM调频广播所用采样率；
32,000 Hz：miniDV 数码视频 camcorder、DAT（LP mode）所用采样率；
44,100 Hz：音频 CD，也常用于 MPEG-1 音频（VCD/SVCD/MP3）所用采样率；
47,250 Hz：商用 PCM 录音机所用采样率；
48,000 Hz：miniDV、数字电视、DVD、DAT、电影和专业音频所用的数字声音所用采样率；
50,000 Hz：商用数字录音机所用采样率；
96,000 或者 192,000 Hz：DVD-Audio、一些 LPCM DVD 音轨、BD-ROM（蓝光盘）音轨、和 HD-DVD（高清晰度DVD）音轨所用所用采样率；
2.8224 MHz：Direct Stream Digital 的 1 位 sigma-delta modulation 过程所用采样率。

2）量化位深

量化位深是对模拟音频信号的幅度轴进行数字化，它决定了模拟信号数字化以后的动态范围。比如，8 bit 位深可以拥有 48 分贝的动态范围，16 bit位深可以拥有 96 分贝的动态范围，24 bit 位深可以拥有 144 分贝的动态范围，32 bit 位深可以拥有 192 分贝的动态范围。这里位深和动态范围的数值对应关系的计算公式可以从上文声压级的计算公式推导而来。位深体现的是能表示的值的范围，比如 16 bit 能表示的最大值是 2^16- 1 = 65535，那么取其最大值就能计算它能表示的最大声压级：最大声压级 = 20 × lg(65535) = 96.33。所以 16 bit 的位深可以最大表示 96 分贝。

所以这个公式是：

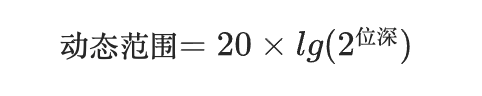
人耳有大约 140 分贝的动态听力范围，类似一根针掉到地上和喷气发动机噪音的区别。当声压级达 120 分贝时，人耳将感到痛楚，无法忍受，因此，人能接受的动态范围为 0～120 分贝。在音乐厅中听乐队演奏大型交响音乐，最响的音乐片段可达 115 分贝，最弱的音乐片段约为 25 分贝，因而动态范围可达 90 分贝。当然，这是很少有的情况。通常交响音乐的动态范围约为 50～80 分贝，中、小型音乐的动态范围约在 40 分贝左右，语言的动态范围约在 30 分贝左右。

CD 音乐音频使用 16 bit 的位深，DVD 音频使用 24 bit 的位深，而大多数电话设备使用 8 bit 的位深。

为了避免运算中声音信号精度的丢失，目前业界高端音频处理系统里都是用 32 bit float 采样来进行运算的，而输出的时候转化为 16 bit。

3）声道

声道是指声音在录制或播放时在不同空间位置采集或回放的相互独立的音频信号，所以声道数也就是声音录制时的音源数量或回放时相应的扬声器数量。

5、数字音频数据是什么？

我们在手机、电脑上处理的声音数据，就是声音经过数字化后的数据，也就是数字音频数据，其中最常见的格式是 PCM（Pulse Code Modulation），即脉冲编码调制格式。得到 PCM 数据的主要过程是将话音等模拟信号每隔一定时间进行取样，使其离散化，同时将抽样值按分层单位四舍五入取整量化，同时将抽样值按一组二进制码来表示抽样脉冲的幅值。也就是我们在上文中讲到的采样、量化、编码过程。

在计算机应用中，PCM 是能达到音频最高保真水平的格式，它被广泛用于素材保存及音乐欣赏，PCM 也因此被称为无损编码格式。但这并不意味着 PCM 就能够确保信号绝对保真，它只能做到最大程度的无限接近原始声音。要计算一个 PCM 音频流的码率需要数字音频的三要素信息即可：码率 = 采样率 × 量化位深 × 声道数。

在处理 PCM 数据时，对于音频不同声道的数据，有两种不同的存储格式：

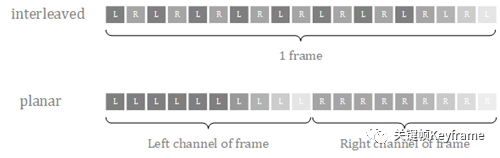
下面是一个示例：

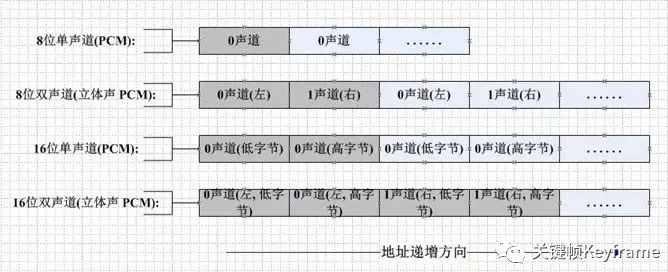
此外，在处理 PCM 数据时，还需要注意大小端字节序类型。

由于 PCM 编码是无损编码，且广泛应用，所以我们通常可以认为音频的裸数据格式就是 PCM 的。但为了节省存储空间以及传输成本，通常我们会对音频 PCM 数据进行压缩，这也就是音频编码，比如 MP3、AAC、OPUS 都是我们常见的音频编码格式。更多关于音频编码的内容，我们将在后面专题介绍。

本文参考

  1. 音高
  2. 音符
  3. 如何理解声强级和声压级
  4. 麦克风是如何采集声音的

（通过上文的探讨，我们知道了对声音进行数字化的过程：采样 → 量化 → 编码，以及数字音频的要素：采样率、量化位深、声道数，我们还知道了 44100 这个奇葩数字的来历。经过数字化过程后，就可以得到我们熟悉的 PCM 数字音频数据了。这些是我们在音视频开发中所熟悉的知识。这样一来，对于『从我们耳朵听见的声音，到我们用手机、电脑所处理的音频数据，其中经历了什么』这个问题的探讨也应该可以暂时告一段落了。我们接下来会继续探讨一些『图像』相关的基础知识，敬请期待）