KMP算法
原文出处：KMP算法
KMP算法（研究总结，字符串）
前段时间学习KMP算法，感觉有些复杂，不过好歹是弄懂啦，简单地记录一下，方便以后自己回忆。
引入
首先我们来看一个例子，现在有两个字符串A和B，问你在A中是否有B，有几个？为了方便叙述，我们先给定两个字符串的值
A="abcaabababaa"
B="abab"
那么普通的匹配是怎么操作的呢？
当然就是一位一位地比啦。（下面用蓝色表示已经匹配，黑色表示匹配失败）
但是我们发现这样匹配很浪费!
为什么这么说呢，我们看到第4步：
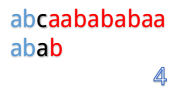
在第4步的时候，我们发现第3位上c与a不匹配，然后第五步的时候我们把B串向后移一位，再从第一个开始匹配。
这里就有一个对已知信息很大的浪费，因为根据前面的匹配结果，我们知道B串的前两位是ab，所以不管怎么移，都是不能和b匹配的,所以应该直接跳过对A串第二位的匹配，对于A串的第三位也是同理。
或许这这个例子还不够经典，我们再举一个。
A="abbaabbbabaa"
B="abbaaba"
在这个例子中，我们依然从第1位开始匹配，直到匹配失败：
abbaabbbabba
abbaaba
我们发现第7位不匹配
那么我们若按照原来的方式继续匹配，则是把B串向后移一位，重新从第一个字符开始匹配
abbaabbbabba
_abbaaba
依然不匹配，那我们就要继续往后移咯。
且住！
既然我们已经匹配了前面的6位，那么我们也就知道了A串这6位和B串的前6位是匹配的，我们能否利用这个信息来优化我们的匹配呢？
也就是说，我们能不能在上面匹配失败后直接跳到：
abbaabbbabba
____abbaaba
这样就可以省去很多不必要的匹配。
KMP算法
KMP算法就是解决上面的问题的，在讲述之前，我们先摆出两个概念：
前缀：指的是字符串的子串中从原串最前面开始的子串，如abcdef的前缀有：a,ab,abc,abcd,abcde
后缀：指的是字符串的子串中在原串结尾处结尾的子串，如abcdef的后缀有：f,ef,def,cdef,bcdef
KMP算法引入了一个F数组（在很多文章中会称为next,但笔者更习惯用F，这更方便表达），F[i]表示的是前i的字符组成的这个子串最长的相同前缀后缀的长度！
怎么理解呢？
例如字符串aababaaba的相同前缀后缀有a和aaba，那么其中最长的就是aaba。
KMP算法的难理解之处与本文叙述的约定
在继续我们的讲述之前，笔者首先讲一下为什么KMP算法不是很好理解。
虽然说网上关于KMP算法的博客、教程很多，但笔者查阅很多资料，详细讲述过程及原理的不多，真正讲得好的文章在定义方面又有细微的不同（当然，真正写得好的文章也有，这里就不一一列举），比如说有些从1开始标号，有些next表示的是前一个而有些是当前的，通读下来，难免会混乱。
那么，为了防止读者在接下来的内容中感到和笔者之前学习时同样的困惑，在这里先对下文做一些说明和约定。
1.本文中，所有的字符串从0开始编号
2.本文中，F数组（即其他文章中的next），F[i]表示0~i的字符串的最长相同前缀后缀的长度。
F数组的运用
那么现在假设我们已经得到了F的所有值，我们如何利用F数组求解呢？
我们还是先给出一个例子（笔者用了好长时间才构造出这一个比较典型的例子啊）：
A="abaabaabbabaaabaabbabaab"
B="abaabbabaab"
当然读者可以通过手动模拟得出只有一个地方匹配
abaabaabbabaaabaabbabaab
那么我们根据手动模拟，同样可以计算出各个F的值
B="a b a a b b a b a a b "
F= 0 0 1 1 2 0 1 2 3 4 5（2017.7.25 Update 这里之前有一个错误，感谢@ 歌古道指正）（2017.7.29 Update 好吧，这里原来还有一个错误，已经更正啦感谢@iwangtst）
我们再用i表示当前A串要匹配的位置（即还未匹配），j表示当前B串匹配的位置（同样也是还未匹配），补充一下，若i>0则说明i-1是已经匹配的啦（j同理）。
首先我们还是从0开始匹配：
此时，我们发现，A的第5位和B的第5位不匹配（注意从０开始编号），此时i=5,j=5，那么我们看F[j-1]的值：
F[5-1]=2;
这说明我们接下来的匹配只要从B串第２位开始（也就是第３个字符）匹配，因为前两位已经是匹配的啦，具体请看图：
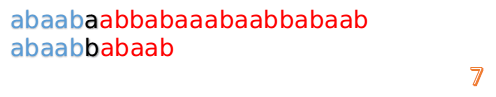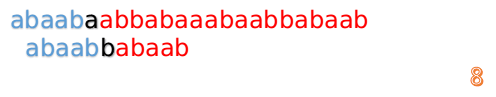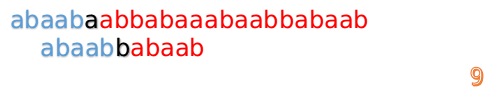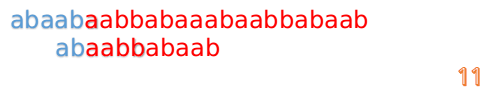
然后再接着匹配：
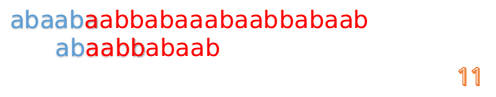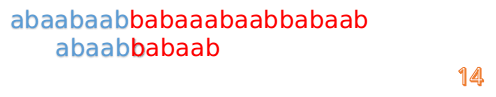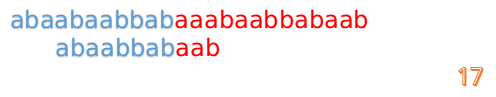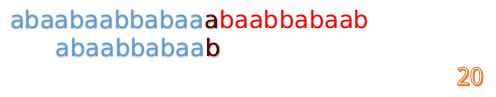
我们又发现，A串的第13位和B串的第10位不匹配，此时i=13,j=10，那么我们看F[j-1]的值：
F[10-1]=4
这说明B串的03位是与当前(i-4)(i-1)是匹配的，我们就不需要重新再匹配这部分了，把B串向后移，从Ｂ串的第４位开始匹配：
这时我们发现A串的第13位和B串的第4位依然不匹配
此时i=13,j=4，那么我们看F[j-1]的值：
F[4-1]=1
这说明B串的第0位是与当前i-1位匹配的，所以我们直接从B串的第1位继续匹配：
但此时B串的第1位与A串的第13位依然不匹配
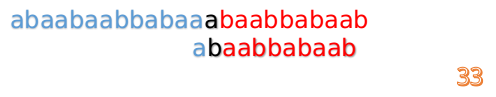
此时，i=13,j=1,所以我们看一看F[j-1]的值:
F[1-1]=0
好吧，这说明已经没有相同的前后缀了，直接把B串向后移一位，直到发现B串的第0位与A串的第i位可以匹配（在这个例子中，i=13）
再重复上面的匹配过程，我们发现，匹配成功了！
这就是KMP算法的过程。
另外强调一点，当我们将B串向后移的过程其实就是i++,而当我们不动B，而是匹配的时候，就是i++,j++，这在后面的代码中会出现，这里先做一个说明。
最后来一个完整版的（话说做这些图做了好久啊！！！！）：
F数组的求解
既然已经用这么多篇幅具体阐述了如何利用F数组求解，那么如何计算出F数组呢？总不能暴力求解吧。
KMP的另外一个巧妙的地方也就在这里，它利用我们上面用B匹配A的方法来计算F数组，简单点来说，就是用B串匹配B串自己！
当然，因为B串==B串，所以如果直接按上面的匹配，那是毫无意义的（自己当然可以完全匹配自己啦），所以这里要变一变。
因为上面已经讲过一部分了，先给出计算F的代码：
for (int i=1;i<m;i++)
{
int j=F[i-1];
while ((B[j+1]!=B[i])&&(j>=0))
j=F[j];
if (B[j+1]==B[i])
F[i]=j+1;
else
F[i]=-1;
}
首先可以确定的几点是：
1.F[0]=-1 (虽说这里应该是０，但为了方便判越界，同时为了方便判断第０位与第i位，程序中这里置为-1)
2.这是一个从前往后的线性推导，所以在计算F[i]时可以保证F[0]~F[i-1]都是已经计算出来的了
3.若以某一位结尾的子串不存在相同的前缀和后缀，这个位的F置为-1（这里置为-1的原因同第一条一样）
重要！：另外，为了在程序中表示方便，在接下来的说明中，F[i]=0表示最长相同前缀后缀长度为１，即真实的最长相同前缀后缀＝F[i]+1。(重要的内容要放大)
为什么要这样设置呢，因为这时F[i]代表的就不仅仅与前后缀长度有关了，它还代表着这个前缀的最后一个字符在子串B中的位置。
所以，之前上面列出的F值要变一下（这里用'_'辅助对齐）：
B="a _b a a b _b a b a a b "
F= -1 -1 0 0 1 -1 0 1 2 3 4
那么，我们同样可以推出，求解F的思路是：看F[i-1]这个最长相同前缀后缀的后面是否可以接i，若可以，则直接接上，若不可以，下面再说。
举个例子：
还是以B="abaabbabaab"为例，我们看到第2个。
B="a b a a b b a b a a b"
F=-1 -1
此时这个a的前一个b的F值为-1，所以此时a不能接在b的后面（b的相同最长前缀后缀是０啊），此时，j=-1，所以我们判断B[j+1]与B[2]，即B[0]与B[2]是否一样。一样，所以F[2]=j+1=0（代表前0~2字符的最长相同前缀后缀的前缀结束处是B[0],长度为0+1=1）。
再来看到第３个：
B="a b a a b b a b a a b"
F=-1 -1 0
开始时,j=F[3-1]=0，我们发现B[j+1=1]!=B[i=3]，所以j=F[j]=-1,此时B[j+1=0]==B[i=3]，所以F[3]=j+1=0。
最后举个例子，看到第４个
B="a b a a b b a b a a b"
F=-1 -1 0 0
j首先为F[4-1]=0，我们看到B[j+1=1]==B[i]，所以F[i]=j+1=1。
后面的就请读者自己慢慢推导了。再强调一遍，我们这样求出来的F值是该最长相同前缀后缀中的前缀的结束字符的数组位置（从０开始编号），如果要求最长相同前缀后缀的长度，要输出F[i]+1。
代码
求解F数组：
for (int i=1;i<m;i++)
{
int j=F[i-1];
while ((B[j+1]!=B[i])&&(j>=0))
j=F[j];
if (B[j+1]==B[i])
F[i]=j+1;
else
F[i]=-1;
}
利用F数组寻找匹配，这里我们是每找到一个匹配就输出其开始的位置：
while (i<n)
{
if (A[i]==B[j])
{
i++;
j++;
if (j==m)
{
printf("%d\n",i-m+1);//注意,这里输出的位置是从1开始标号的,如果你要输出从0开始标号的位置,应该是是i-m.这份代码是我做一道题时写的,那道题要求输出的字符串位置从1开始标号.感谢@Draymonder指出了这个疏漏,更多内容请看评论区
j=F[j-1]+1;
}
}
else
{
if (j==0)
i++;
else
j=F[j-1]+1;
}
}
以下内容 Update at 2019.4.26
贴一个现在自己的写法，不过这里字符串是从 1 开始标号的，如果上面理解了的话不难转化。
Nxt[0]=Nxt[1]=0;
for (int i=2,j=0;i<=m;i++){//构建 Next
while (j&&T[j+1]!=T[i]) j=Nxt[j];
if (T[j+1]==T[i]) ++j;Nxt[i]=j;
}
for (int i=1,j=0;i<=n;i++){//匹配
while (j&&T[j+1]!=S[i]) j=Nxt[j];
if (T[j+1]==S[i]) ++j;
if (j==m) Mch[i]=1,j=Nxt[j];//匹配成功
}
自己选择的路，跪着也要走完。朋友们，虽然这个世界日益浮躁起来，只要能够为了当时纯粹的梦想和感动坚持努力下去，不管其它人怎么样，我们也能够保持自己的本色走下去。
原文出处：重学KMP！
28. 实现 strStr()
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置(从0开始)。如果不存在，则返回 -1。
示例 1: 输入: haystack = "hello", needle = "ll" 输出: 2
示例 2: 输入: haystack = "aaaaa", needle = "bba" 输出: -1
说明: 当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。对于本题而言，当 needle 是空字符串时我们应当返回 0。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。
思路
本题是KMP 经典题目，通过道题题目我们把来把KMP彻底讲清楚。
以下文字如果看不进去，可以看我的B站视频，再结合本篇文章来看，相信可以解决你对KMP算法的所有疑惑！
KMP的经典思想是:当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。
本篇将以如下顺序来讲解KMP，
- 什么是KMP
- KMP有什么用
- 什么是前缀表
- 为什么一定要用前缀表
- 如何计算前缀表
- 前缀表与next数组
- 使用next数组来匹配
- 时间复杂度分析
- 构造next数组
- 使用next数组来做匹配
- 前缀表统一减一 代码实现
- 前缀表（不减一）代码实现
- 总结
什么是KMP
说到KMP，先说一下KMP这个名字是怎么来的，为什么叫做KMP呢。
因为是由这三位学者发明的：Knuth，Morris和Pratt，所以取了三位学者名字的首字母。所以叫做KMP
KMP有什么用
KMP主要应用在字符串匹配上。
KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。
所以如何记录已经匹配的文本内容，是KMP的重点，也是next数组肩负的重任。
其实KMP的代码不好理解，一些同学甚至直接把KMP代码的模板背下来。
没有彻底搞懂，懵懵懂懂就把代码背下来太容易忘了。
不仅面试的时候可能写不出来，如果面试官问：next数组里的数字表示的是什么，为什么这么表示？
估计大多数候选人都是懵逼的。
下面Carl就带大家把KMP的精髓，next数组弄清楚。
什么是前缀表
写过KMP的同学，一定都写过next数组，那么这个next数组究竟是个啥呢？
next数组就是一个前缀表（prefix table）。
前缀表有什么作用呢？
前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。
为了清楚的了解前缀表的来历，我们来举一个例子：
要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。
请记住文本串和模式串的作用，对于理解下文很重要，要不然容易看懵。所以说三遍：
要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。
要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。
要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。
如动画所示：
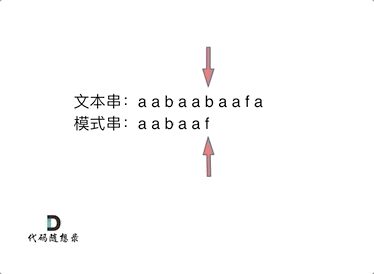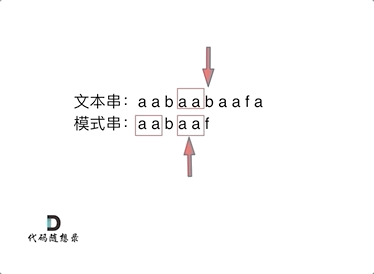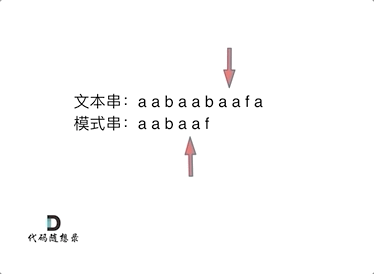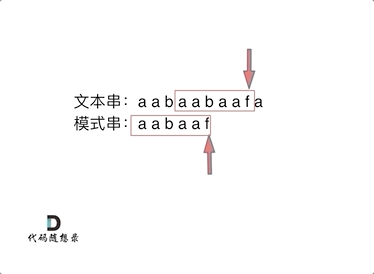
动画里，我特意把 子串aa 标记上了，这是有原因的，大家先注意一下，后面还会说道。
可以看出，文本串中第六个字符b 和 模式串的第六个字符f，不匹配了。如果暴力匹配，会发现不匹配，此时就要从头匹配了。
但如果使用前缀表，就不会从头匹配，而是从上次已经匹配的内容开始匹配，找到了模式串中第三个字符b继续开始匹配。
此时就要问了前缀表是如何记录的呢？
首先要知道前缀表的任务是当前位置匹配失败，找到之前已经匹配上的位置，在重新匹配，此也意味着在某个字符失配时，前缀表会告诉你下一步匹配中，模式串应该跳到哪个位置。
那么什么是前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。
最长公共前后缀？
文章中字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
正确理解什么是前缀什么是后缀很重要!
那么网上清一色都说 “kmp 最长公共前后缀” 又是什么回事呢？
我查了一遍 算法导论 和 算法4里KMP的章节，都没有提到 “最长公共前后缀”这个词，也不知道从哪里来了，我理解是用“最长相等前后缀” 更准确一些。
因为前缀表要求的就是相同前后缀的长度。
而最长公共前后缀里面的“公共”，更像是说前缀和后缀公共的长度。这其实并不是前缀表所需要的。
所以字符串a的最长相等前后缀为0。字符串aa的最长相等前后缀为1。字符串aaa的最长相等前后缀为2。等等.....。
为什么一定要用前缀表
这就是前缀表那为啥就能告诉我们 上次匹配的位置，并跳过去呢？
回顾一下，刚刚匹配的过程在下标5的地方遇到不匹配，模式串是指向f，如图：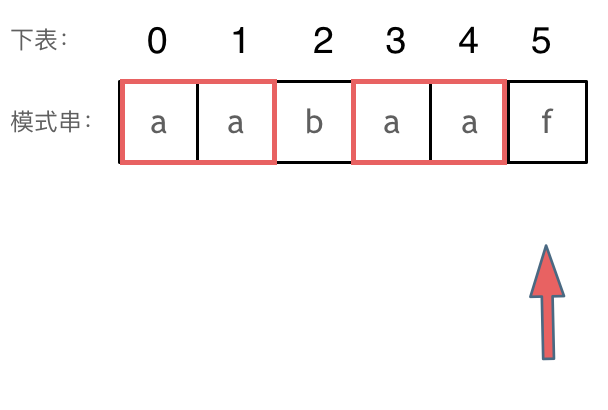
然后就找到了下标2，指向b，继续匹配：如图：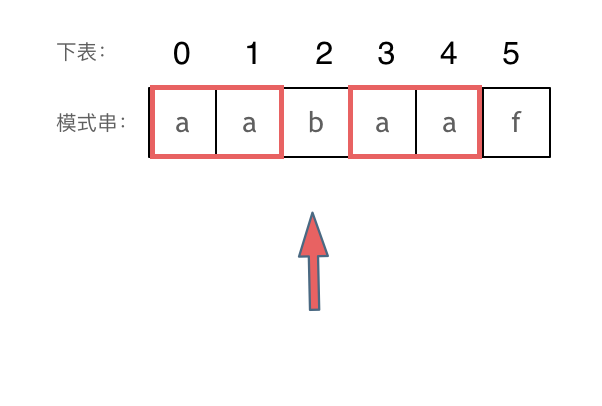
以下这句话，对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要！
下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀 和 后缀字符串是 子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面从新匹配就可以了。
所以前缀表具有告诉我们当前位置匹配失败，跳到之前已经匹配过的地方的能力。
很多介绍KMP的文章或者视频并没有把为什么要用前缀表？这个问题说清楚，而是直接默认使用前缀表。
如何计算前缀表
接下来就要说一说怎么计算前缀表。
如图：
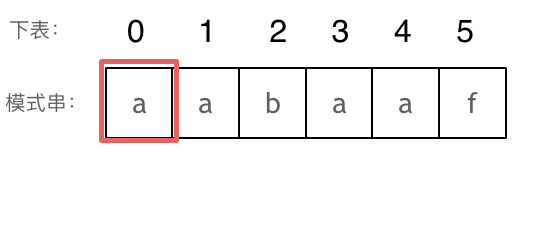
长度为前1个字符的子串a，最长相同前后缀的长度为0。（注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。）
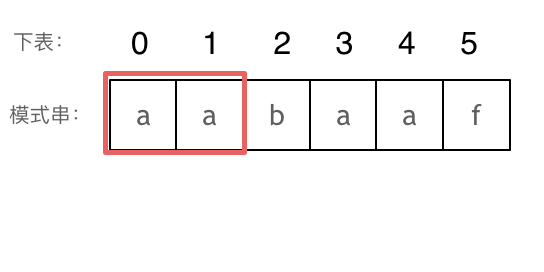长度为前2个字符的子串aa，最长相同前后缀的长度为1。
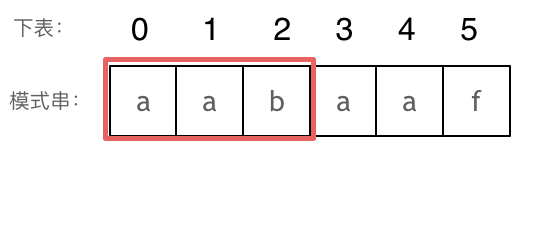长度为前3个字符的子串aab，最长相同前后缀的长度为0。
以此类推：长度为前4个字符的子串aaba，最长相同前后缀的长度为1。长度为前5个字符的子串aabaa，最长相同前后缀的长度为2。长度为前6个字符的子串aabaaf，最长相同前后缀的长度为0。
那么把求得的最长相同前后缀的长度就是对应前缀表的元素，如图：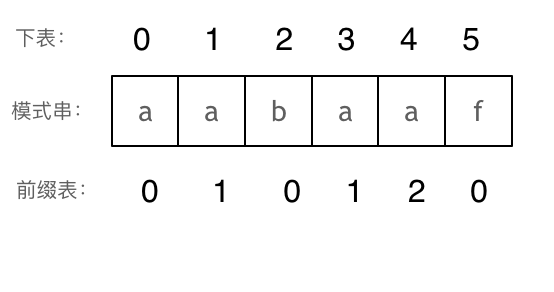
可以看出模式串与前缀表对应位置的数字表示的就是：下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示：
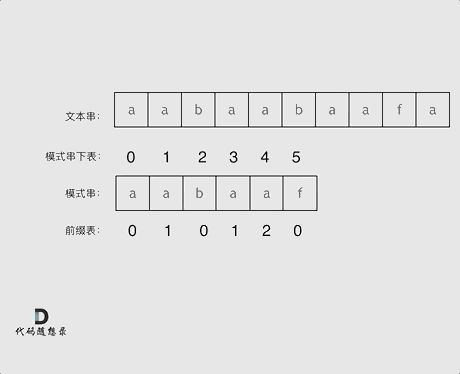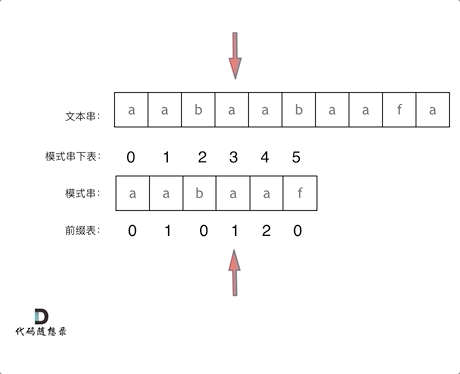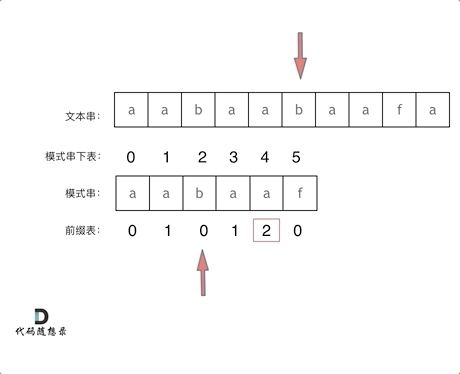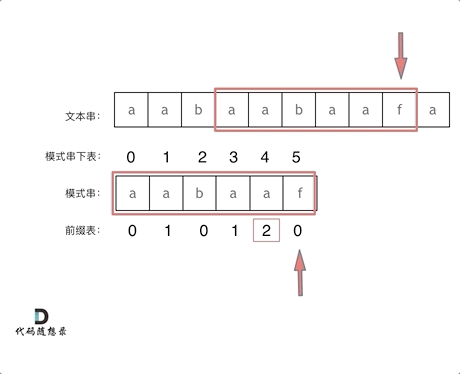
找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。
为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀。
所以要看前一位的 前缀表的数值。
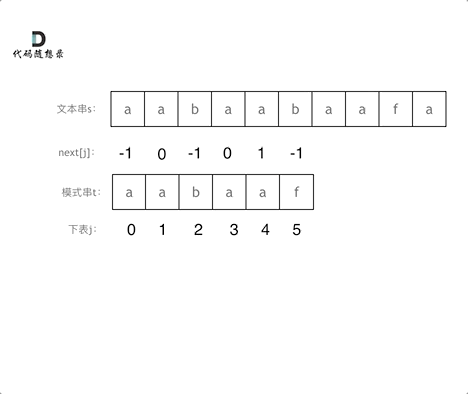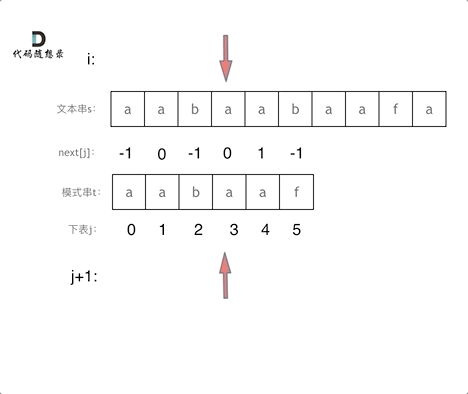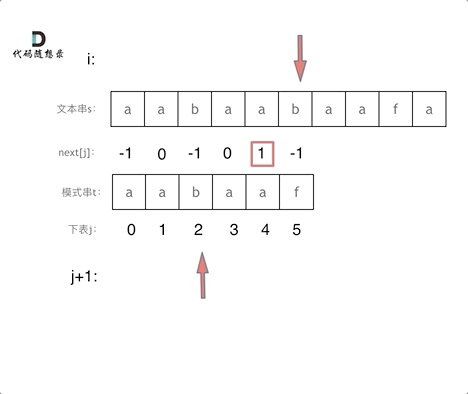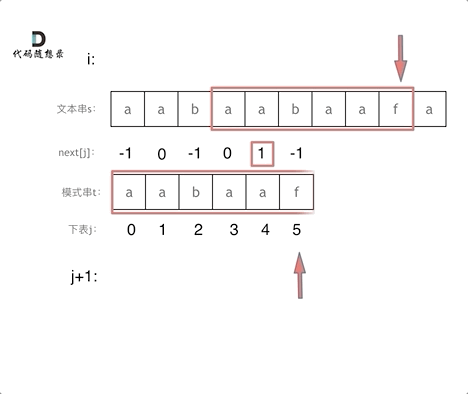
前一个字符的前缀表的数值是2， 所有把下标移动到下标2的位置继续比配。可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
前缀表与next数组
很多KMP算法的时间都是使用next数组来做回退操作，那么next数组与前缀表有什么关系呢？
next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。
为什么这么做呢，其实也是很多文章视频没有解释清楚的地方。
其实这并不涉及到KMP的原理，而是具体实现，next数组即可以就是前缀表，也可以是前缀表统一减一（右移一位，初始位置为-1）。
后面我会提供两种不同的实现代码，大家就明白了了。
使用next数组来匹配
以下我们以前缀表统一减一之后的next数组来做演示。
有了next数组，就可以根据next数组来 匹配文本串s，和模式串t了。
注意next数组是新前缀表（旧前缀表统一减一了）。
匹配过程动画如下：
时间复杂度分析
其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
暴力的解法显而易见是O(n m)，所以*KMP在字符串匹配中极大的提高的搜索的效率。
为了和力扣题目28.实现strStr保持一致，方便大家理解，以下文章统称haystack为文本串, needle为模式串。
都知道使用KMP算法，一定要构造next数组。
构造next数组
我们定义一个函数getNext来构建next数组，函数参数为指向next数组的指针，和一个字符串。代码如下：
void getNext(int* next, const string& s)
构造next数组其实就是计算模式串s，前缀表的过程。 主要有如下三步：
- 初始化
- 处理前后缀不相同的情况
- 处理前后缀相同的情况
接下来我们详解详解一下。
- 初始化：
定义两个指针i和j，j指向前缀起始位置，i指向后缀起始位置。
然后还要对next数组进行初始化赋值，如下：
int j = -1;
next[0] = j;
j 为什么要初始化为 -1呢，因为之前说过前缀表要统一减一的操作仅仅是其中的一种实现，我们这里选择j初始化为-1，下文我还会给出j不初始化为-1的实现代码。
next[i] 表示 i（包括i）之前最长相等的前后缀长度（其实就是j）
所以初始化next[0] = j 。
- 处理前后缀不相同的情况
因为j初始化为-1，那么i就从1开始，进行s[i] 与 s[j+1]的比较。
所以遍历模式串s的循环下标i 要从 1开始，代码如下：
for(int i = 1; i < s.size(); i++) {
如果 s[i] 与 s[j+1]不相同，也就是遇到 前后缀末尾不相同的情况，就要向前回退。
怎么回退呢？
next[j]就是记录着j（包括j）之前的子串的相同前后缀的长度。
那么 s[i] 与 s[j+1] 不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）。
所以，处理前后缀不相同的情况代码如下：
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
- 处理前后缀相同的情况
如果s[i] 与 s[j + 1] 相同，那么就同时向后移动i 和j 说明找到了相同的前后缀，同时还要将j（前缀的长度）赋给next[i],因为next[i]要记录相同前后缀的长度。
代码如下：
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j;
最后整体构建next数组的函数代码如下：
void getNext(int* next, const string& s){
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j（前缀的长度）赋给next[i]
}
}
代码构造next数组的逻辑流程动画如下：
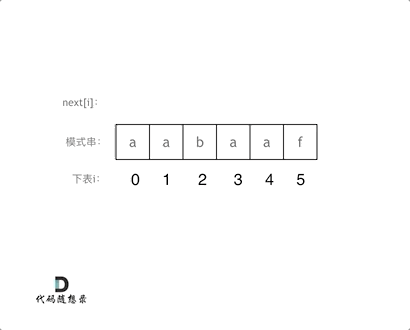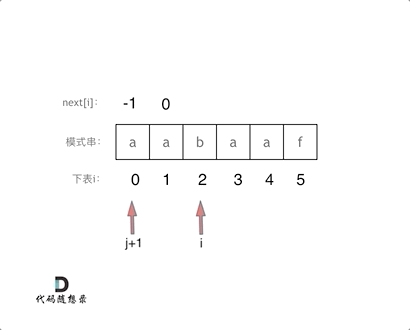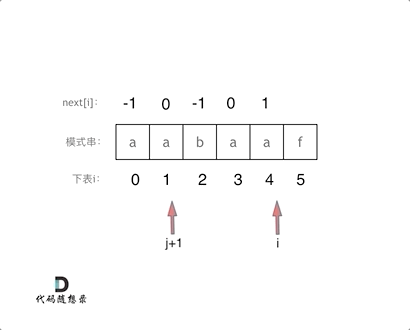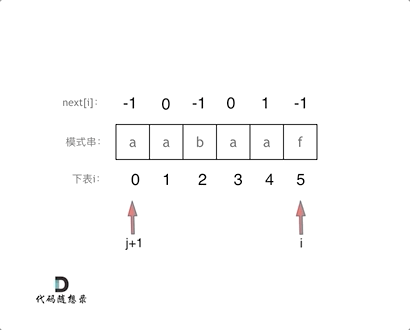
得到了next数组之后，就要用这个来做匹配了。
使用next数组来做匹配
在文本串s里 找是否出现过模式串t。
定义两个下标j 指向模式串起始位置，i指向文本串起始位置。
那么j初始值依然为-1，为什么呢？依然因为next数组里记录的起始位置为-1。
i就从0开始，遍历文本串，代码如下：
for (int i = 0; i < s.size(); i++)
接下来就是 s[i] 与 t[j + 1] （因为j从-1开始的） 进行比较。
如果 s[i] 与 t[j + 1] 不相同，j就要从next数组里寻找下一个匹配的位置。
代码如下：
while(j >= 0 && s[i] != t[j + 1]) {
j = next[j];
}
如果 s[i] 与 t[j + 1] 相同，那么i 和 j 同时向后移动， 代码如下：
if (s[i] == t[j + 1]) {
j++; // i的增加在for循环里
}
如何判断在文本串s里出现了模式串t呢，如果j指向了模式串t的末尾，那么就说明模式串t完全匹配文本串s里的某个子串了。
本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始)，所以返回当前在文本串匹配模式串的位置i 减去模式串的长度，就是文本串字符串中出现模式串的第一个位置。
代码如下：
if (j == (t.size() - 1) ) {
return (i - t.size() + 1);
}
那么使用next数组，用模式串匹配文本串的整体代码如下：
int j = -1; // 因为next数组里记录的起始位置为-1
for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
j = next[j]; // j 寻找之前匹配的位置
}
if (s[i] == t[j + 1]) { // 匹配，j和i同时向后移动
j++; // i的增加在for循环里
}
if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
return (i - t.size() + 1);
}
}
此时所有逻辑的代码都已经写出来了，力扣 28.实现strStr 题目的整体代码如下：
前缀表统一减一 C++代码实现
class Solution {
public:
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j（前缀的长度）赋给next[i]
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) {
return 0;
}
int next[needle.size()];
getNext(next, needle);
int j = -1; // // 因为next数组里记录的起始位置为-1
for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
j = next[j]; // j 寻找之前匹配的位置
}
if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动
j++; // i的增加在for循环里
}
if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
return (i - needle.size() + 1);
}
}
return -1;
}
};
前缀表（不减一）C++实现
那么前缀表就不减一了，也不右移的，到底行不行呢？
行！
我之前说过，这仅仅是KMP算法实现上的问题，如果就直接使用前缀表可以换一种回退方式，找j=next[j-1] 来进行回退。
主要就是j=next[x]这一步最为关键！
我给出的getNext的实现为：（前缀表统一减一）
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j（前缀的长度）赋给next[i]
}
}
此时如果输入的模式串为aabaaf，对应的next为-1 0 -1 0 1 -1。
这里j和next[0]初始化为-1，整个next数组是以 前缀表减一之后的效果来构建的。
那么前缀表不减一来构建next数组，代码如下：
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for(int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
此时如果输入的模式串为aabaaf，对应的next为 0 1 0 1 2 0，（其实这就是前缀表的数值了）。
那么用这样的next数组也可以用来做匹配，代码要有所改动。
实现代码如下：
class Solution {
public:
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for(int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) {
return 0;
}
int next[needle.size()];
getNext(next, needle);
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) {
j = next[j - 1];
}
if (haystack[i] == needle[j]) {
j++;
}
if (j == needle.size() ) {
return (i - needle.size() + 1);
}
}
return -1;
}
};
总结
我们介绍了什么是KMP，KMP可以解决什么问题，然后分析KMP算法里的next数组，知道了next数组就是前缀表，再分析为什么要是前缀表而不是什么其他表。
接着从给出的模式串中，我们一步一步的推导出了前缀表，得出前缀表无论是统一减一还是不减一得到的next数组仅仅是kmp的实现方式的不同。
其中还分析了KMP算法的时间复杂度，并且和暴力方法做了对比。
然后先用前缀表统一减一得到的next数组，求得文本串s里是否出现过模式串t，并给出了具体分析代码。
又给出了直接用前缀表作为next数组，来做匹配的实现代码。
可以说把KMP的每一个细微的细节都扣了出来，毫无遮掩的展示给大家了！
其他语言版本
java:
// 方法一:前缀表使用减1实现
class Solution {
public void getNext(int[] next, String s){
int j = -1;
next[0] = j;
for (int i = 1; i<s.length(); i++){
while(j>=0 && s.charAt(i) != s.charAt(j+1)){
j=next[j];
}
if(s.charAt(i)==s.charAt(j+1)){
j++;
}
next[i] = j;
}
}
public int strStr(String haystack, String needle) {
if(needle.length()==0){
return 0;
}
int[] next = new int[needle.length()];
getNext(next, needle);
int j = -1;
for(int i = 0; i<haystack.length();i++){
while(j>=0 && haystack.charAt(i) != needle.charAt(j+1)){
j = next[j];
}
if(haystack.charAt(i)==needle.charAt(j+1)){
j++;
}
if(j==needle.length()-1){
return (i-needle.length()+1);
}
}
return -1;
}
}
Python：
# 方法一:前缀表使用减1实现
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
a=len(needle)
b=len(haystack)
if a==0:
return 0
next=self.getnext(a,needle)
p=-1
for j in range(b):
while p>=0 and needle[p+1]!=haystack[j]:
p=next[p]
if needle[p+1]==haystack[j]:
p+=1
if p==a-1:
return j-a+1
return -1
def getnext(self,a,needle):
next=['' for i in range(a)]
k=-1
next[0]=k
for i in range(1,len(needle)):
while (k>-1 and needle[k+1]!=needle[i]):
k=next[k]
if needle[k+1]==needle[i]:
k+=1
next[i]=k
return next
# 方法二: 前缀表无减一或者右移
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
a=len(needle)
b=len(haystack)
if a==0:
return 0
i=j=0
next=self.getnext(a,needle)
while(i<b and j<a):
if j==-1 or needle[j]==haystack[i]:
i+=1
j+=1
else:
j=next[j]
if j==a:
return i-j
else:
return -1
def getnext(self,a,needle):
next=['' for i in range(a)]
j,k=0,-1
next[0]=k
while(j<a-1):
if k==-1 or needle[k]==needle[j]:
k+=1
j+=1
next[j]=k
else:
k=next[k]
return next